


Gisbert Stoyan, ELTE Budapest
Die Velte-Zerlegung des Sobolev-Raumes
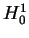 und einige Anwendungen
und einige Anwendungen
Abstract:
Im Jahr 1990 veröffentlichte W. Velte eine Zerlegung des Sobolev-Raumes
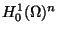 (mit
(mit 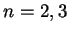 )
in drei orthogonale Unterräume, die an die
klassische Helmholtz-Zerlegung erinnert; sie ist
mit einer Zerlegung des Raumes
)
in drei orthogonale Unterräume, die an die
klassische Helmholtz-Zerlegung erinnert; sie ist
mit einer Zerlegung des Raumes
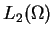 verbunden, deren dritter
Teilraum aus harmonischen Funktionen besteht. Hier ist
verbunden, deren dritter
Teilraum aus harmonischen Funktionen besteht. Hier ist 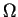 ein lipschitzstetiges Gebiet im
ein lipschitzstetiges Gebiet im
![]() .
.
Wir zeigen die Verbindung der Velte-Zerlegung zur Stabilitätsbedingung
der Stokesschen Randwertaufgabe, bringen konkrete Informationen über die
inf-sup-Konstante in Abhängigkeit von ![]() ,
geben
Diskretisierungen des Stokes-Problems an, die eine diskrete Velte-Zerlegung
garantieren und leiten optimale Parameter für die
Uzawa- und Arrow-Hurwitz-Verfahren her, die in Spezialfällen eine schnellere
Konvergenz ergeben als neue, speziell für Sattelpunktprobleme
vorkonditionierte Iterationsverfahren.
,
geben
Diskretisierungen des Stokes-Problems an, die eine diskrete Velte-Zerlegung
garantieren und leiten optimale Parameter für die
Uzawa- und Arrow-Hurwitz-Verfahren her, die in Spezialfällen eine schnellere
Konvergenz ergeben als neue, speziell für Sattelpunktprobleme
vorkonditionierte Iterationsverfahren.
Literatur
W. Velte
On optimal constants in some inequalities,
in: The Navier-Stokes Equations; Theory and Numerical Methods
(J.G. Heywood et al., eds.). Lecture Notes in Math. 1431,
pp. 158--168. Berlin: Springer 1990.
G. Stoyan
Towards discrete Velte decompositions and narrow
bounds for inf-sup constants,
Computers & Maths. with Appls., 38, 7-8 (1999), 243--261.
| Zeit: | Freitag, 14. Januar 2000, 14.15 Uhr |
| Ort: | FU Berlin, Arnimallee 2-6, Raum 032 im EG |

