Matheon Project C-SE12

FU Berlin ECMath Matheon

Fast solvers for heterogeneous saddle point problems

This research is carried out in the framework of Matheon supported by Einstein Foundation Berlin.

Project id Matheon project C-SE12
Project head Carsten Gräser (FU Berlin)
Project staff -
Funding Project funded by Einstein Center for Mathematics Berlin
Funding period 2014-06 - 2017-05

Objective

The aim of this project is to develop fast solvers for heterogeneous linear saddle point problems as appearing during the iterative solution of non-smooth optimization problems, e.g., in the context of phase field models. While the development of nonlinear solvers for phase field models has reached a certain maturity, the existing solvers for the linear subproblems are still unsatisfactory. As a first step, we focus on two-phase models. Later, we plan to extend these solvers for multiphase systems.

Description

Large scale nonsmooth nonlinear saddle point problems occur, e.g., in the context of 4th order phase field models or optimal control problems for partial differential equations. Semi-smooth or nonsmooth Newton methods have shown to be highly efficient for the iterative solution of such problems. These methods can typically be viewed as active set type strategies that lead to large linear saddle point problems as subproblems. Resulting from these active-set strategies, the subproblems are typically constrained to subsets of the domain for the primal equation. As a consequence, they can be viewed as hybrid problems that have saddle point structure only in some part of the domain, while they are elliptic in other parts. Another feature of these problems is, that they can be viewed as singularly perturbed problems, because they typically depend on small parameters, resulting, e.g., from the interface thickness in the phase field model or the regularization parameter in an optimal control problem.

While there has been significant progress on the development of fast solvers for nonsmooth nonlinear saddle point problems, the efficient solution of the resulting hybrid linear saddle point subproblems has seen far less progress. E.g., in the context of phase field problems, classical multigrid methods typically lack robustness with respect to the subdomain. As a consequence the solution of such hybrid saddle point problems is the bottle neck in real simulations of application projects.

The project aim is to support application projects by closing this gap and developing efficient solvers for those subproblems. We are especially in cooperation with the Helmholtz Virtual Institute „Microstructure control for thin film solar cells“ (HVI) where highly efficient numerical methods are crucial for the carried out simulations.

Highlights

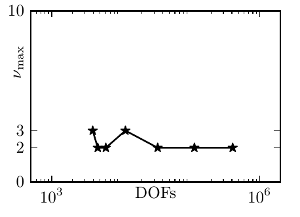
Because the known nonlinear solvers turned out to lack efficiency for the problems considered in subprojekt 6 of the HVI we extended the nonsmooth Schur-Newton method to the nonsmooth nonlinear saddle point problems with simplex constraints in cooperation with this project. The developed method exhibits mesh independent convergence and allows to solve the multi-component phase field problems considered in the HVI very efficiently (2). Since the method is a dual minimization method it leads to primal minimization problems with simplex constraints. However, such problems can be solved with multigrid efficiency using the TNNMG method (5).

Figure: Nonsmooth Schur-Newton steps over mesh size for a multi-component Penrose-Fife model and result of an LPC simulation based on the Penrose-Fife model:

Project publications

Other publications

Talks

Software

We contribute to the development of the Dune software library for highly efficient grid based methods for PDEs which especially incorporates the following dune modules:

Cooperations

Internal

External