Prof. Dr. Igor Podlubny
U Kosice, Slowakei
On a Parallel Method for Initial and Boundary Value Problems for Linear Ordinary Differential Equations and Their Systems
Abstract:
The proposed method is based on deviding a problem in similar so-called
local problems, which can be solved independently and in parallel using
any known method. The solution is then built as a linear combination of the
obtained local solutions (i.e. solutions of local problems).
The recurrence relationships (in case of non-homogeneous equations) and
explicit expressions (in case of homogeneous equations) for the coefficients
of the above-mentioned linear combination are obtained. The speed-up of
the proposed method is considered for some particular methods, used for
solving the local problems, as well as the problem of determination of the
optimal number of sub-intervals (or processors) and the optimal number
of equidistant nodes in each sub-interval. It is proved that the method
speed-up
is proportional to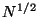 
, where N is the total number of equidistant
nodes.
The idea of the method and the speed-up estimation is illustrated by
several
elementary examples.
| Zeit: | Freitag, 10. Dezember 1999, 14.15 Uhr |
| Ort: | FU Berlin, Arnimallee 2-6, Raum 032 im EG |