• The Technological Challenge
• The Goal
• The Means
  • The Phase Field Model
  • Analysis
  • Numerics - Fast Multigrid Methods
• References

The heaps of electronic waste produced by modern societies - among other toxic substances - contain highly toxic lead in the form of tin(Sn)/lead(Pb)-alloy in the solderjoints fixing chips, condensators etc to the circuit boards. Via this channel some 20.000 metric tons of lead are distributed each year. For environmental and health reasons there is world wide pressure on the industry to eliminate lead from electronic devices. By July 2006 the use of lead in noncritical appliances was banned in the EU. Hence alternative lead-free solder-alloys such as SnAg, CuSn, SnAgCu have to be developed and put to the test. The main issue is solder-joint reliability as under thermomechanical stress a demixing of alloys occurs leading to cracks in the solder and thus to joint failure ultimately resulting in the failure of the electronic component.

Aging of Ag71Cu29 alloy after 2h, 5h, 40h at 970 K (pictures courtesy of Müller/Böhme, TU Berlin)

The goal of this project is the reliable and efficient numerical simulation of these phase-separation processes in order to make life-span predictions for different setups.

• The phase field model
• Analysis
• Numerics - Fast Multigrid Methods

The Phase Field Model

Our approach to phase separation is by phase field models introducing the order parameter (or phase field) c with c(x)∈[0,1] ∀x∈Ω, describing the concentrations of the species at each point. Furthermore we consider linear elastic effects for which a strain field ε is introduced. The free energy of the system is given by E(c,ε)=∫ψ(c)+φ(c)+W(c,ε) dx where the double-well potential ψ is driving phase separation whereas the interaction term φ describes interface motion. W accounts for elastic effects due to e.g. lattice misfits, different thermal expansion, external stresses etc.

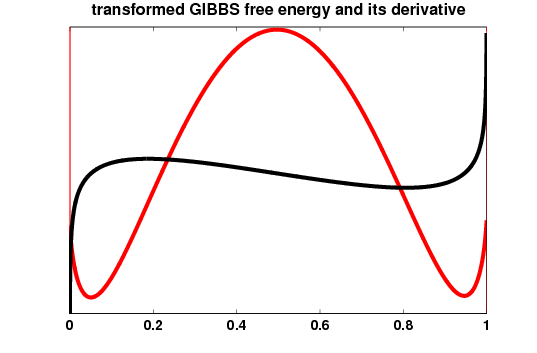The double-well potential ψ is modelled by logarithmic terms in the like of ψ(c)=θ[(1-c)ln((1-c))+cln(c)] + Θ/2(1-c²) and has two distinct local minima once the temperature θ drops below the critical temperature Θ. In the theoretical analysis we focus on nonlocal interaction terms whereas for the numerical simulations local interaction terms are assumed as appearing in the models by Dreyer/Müller/Böhme [1, 2].

Analysis

Establishing existence (and possibly uniqueness) of solutions to the continuous system is of prime importance in the theoretical treatment of the equations and justifies a numerical search for solutions. As mentioned before, our analytic efforts focus on systems with a non-local interaction term. Our analysis extends further to the non-isothermal case [3, 4].

Numerics - Fast Multigrid Methods

Following Rothe's method we first discretize in time. The spatial problems resulting from implicit time discretization find a reformulation as a nonlinear saddle-point problem. Space discretization is done by P1-Finite Elements. A preconditioned Uzawa algorithm for the nonlinear saddle-point problem leaves us with a linear saddle-point problem and an Allen-Cahn-type problem to solve. Here we exploit the convexity rather than (the potentially nonexistent) smoothness of the energy functional in order to find a minimum via a descent method. To be more precise we use a nonlinear Gauss-Seidel algorithm as fine-grid smoother and a globally damped modification of constrained Newton linearization for the coarse grid corrections [5, 6].
The typical structure of the solutions strongly suggests adaptive strategies in space and time.

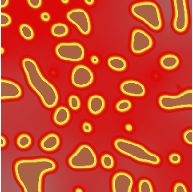
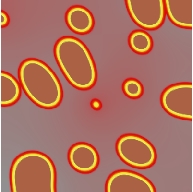Simulation for a AgCu alloy with realistic material parameters

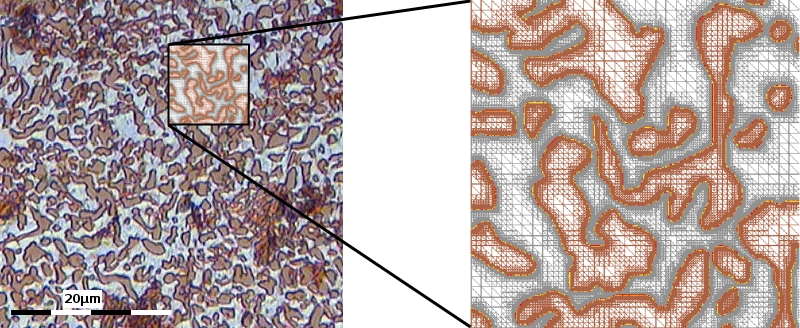Solution and computational grid for first time step, initial data taken from experiment

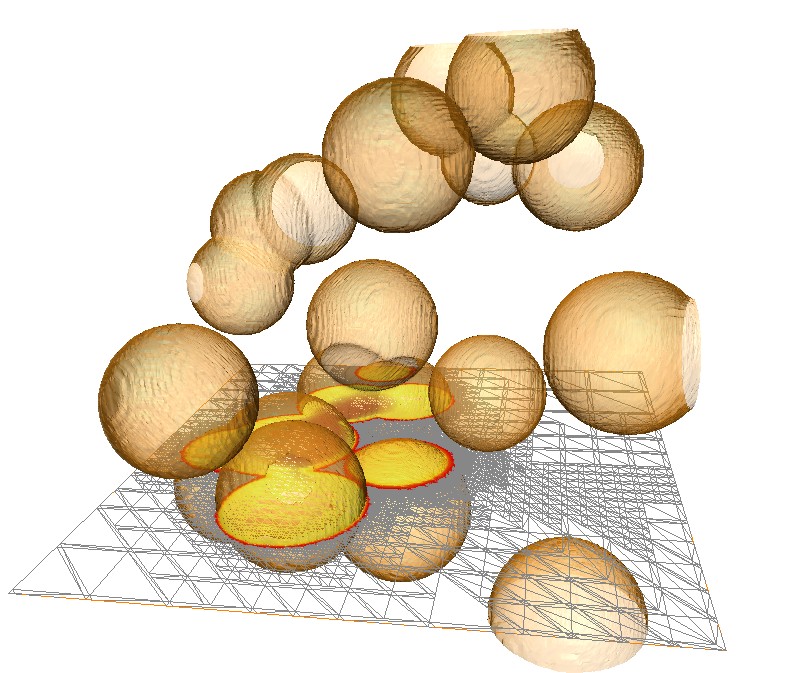Isosurface of the solution and cross-section of computational grid for first time step in three space dimensions